新方法!解决多电平双有源桥变换器的电感电流有效值最优跟踪问题
New method! Solving the optimal tracking problem of inductance current effective value in multilevel dual active bridge converters
研究背景
双有源桥(Dual-Active Bridge, DAB)变换器具有输入输出电气隔离、高功率密度、能量双向流动等优点,在分布式发电、电动汽车、直流配电网等领域有着广泛的应用。传统的两电平DAB采用扩展移相、双移相和三移相控制,通过增加控制自由度,从减小电流应力、降低回流功率、实现ZVS等方面进行优化。增加控制自由度的另一个措施是采用多电平DAB结构,不仅能够扩展输入和输出电压范围,而且低耐压的功率器件能够降低装置成本和开关损耗。
为提高变换效率,希望DAB在传递相同功率的情况下电感电流应力或有效值最小。传统的DAB电感电流应力优化策略,通常得到各功率区段移相比与传输功率、电压传输比的解析关系,根据传输功率所在区段和电压传输比,选择相应的移相比,这种优化方法没有考虑变换器中存在的杂散电阻损耗和开关损耗对传输功率的影响,近似将输出功率等同于传输功率,实际工作的最优点将会偏离理想最优点。且电感电流有效值表达式较复杂,通常无法直接得到移相比与传输功率以及电压传输比的关系。因此,有必要研究能够克服杂散损耗对电感电流有效值最小工作点影响的优化方法。
论文所解决的问题及意义
福州大学科研团队为了解决杂散电阻损耗和开关损耗对DAB最优工作点的影响,提出一种三电平扩展移相下电感电流有效值最小工作点跟踪控制策略,能够克服杂散电阻和开关损耗对最优工作点的影响,使变换器能够时刻跟踪最优工作点。
论文方法及创新点
三电平DAB电路结构和三电平扩展移相控制策略如图1所示。
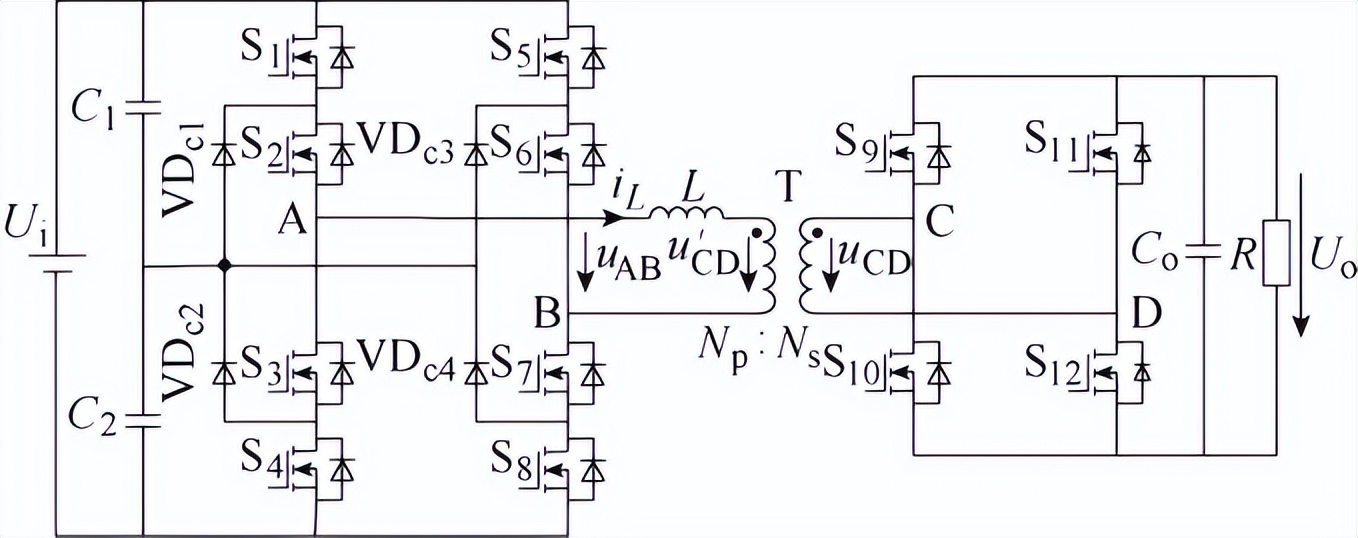
(a)电路结构
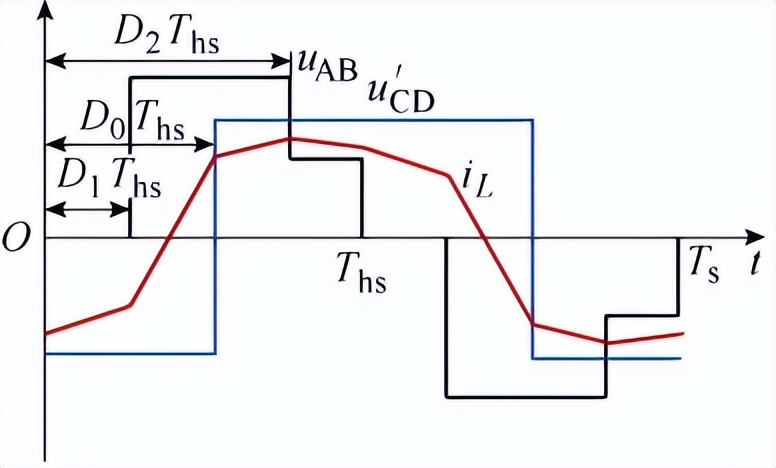
图1 三电平DAB电路结构和三电平扩展移相控制原理波形
首先根据Lagrange乘数法,可得目标函数Iib_rms2在约束条件Pbi(D0,D1,D2)-Pb=0下的内部极值点处三个移相比之间的解析关系,即在内部极值点处将D0、D1分别表示为D2的函数,根据该工作模式的约束条件得到内部各极值点处移相比和传输功率的范围;
然后比较内部最优极值点和边界最优点处电感电流有效值,内部最优极值点总是优于边界最优极值点,因此全局最优工作点就是内部最优极值点;最后,在各全局最优工作点处将传输功率表示为D2的函数,即Pb(k,D2),得到Pb(k,D2)对D2的偏导数如图2所示。
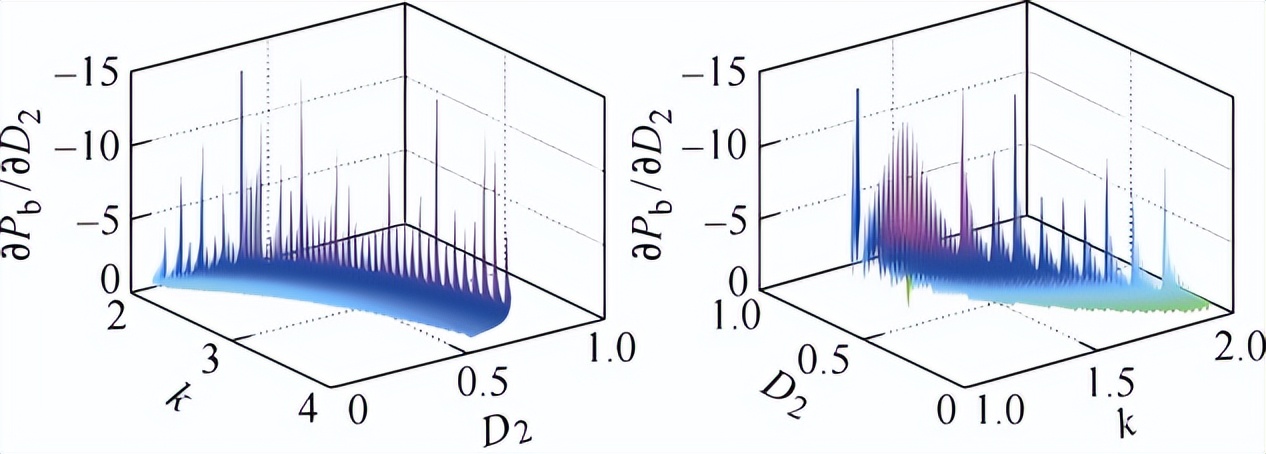
(a)解a1 (b)解a3
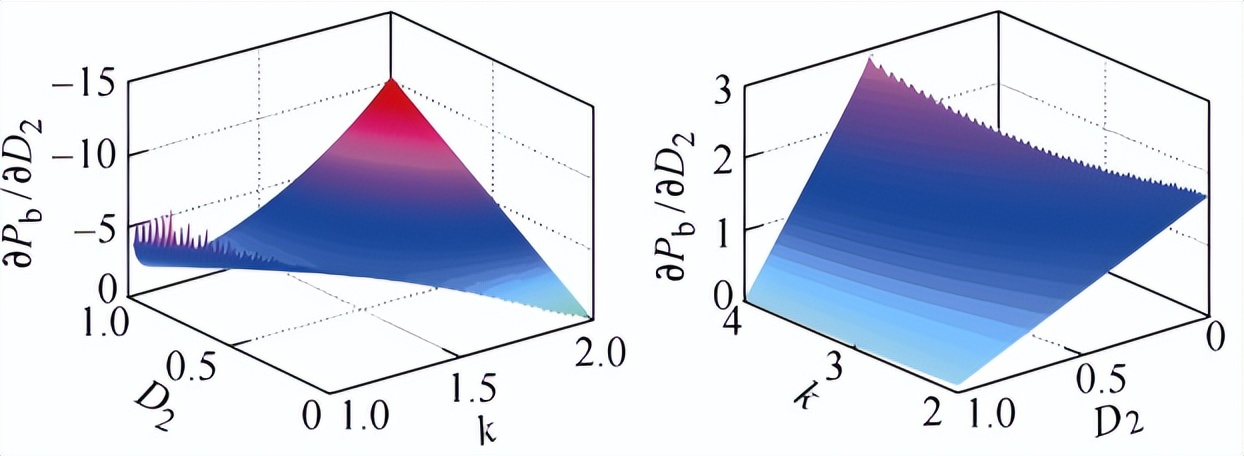
(c)解b2 (d)解b3
图2 4个最优解对应的∂Pb(k, D2)/∂D2
由图2可知,对于解a1和解a3,在对应的 (k, D2) 取值区域内,∂Pb(k, D2)/∂D2<0,说明在最优解a1和解a3下,Pb与D2呈负相关,解a1和解a3对应的最优解模式应采用负PI进行调节;对于解b2和解b3,在对应的 (k, D2) 取值区域内,∂Pb(k, D2)/∂D2>0,Pb与D2呈正相关,解b2和解b3对应的最优解模式应采用正PI进行调节。全局最优工作点跟踪控制框图如图3所示。
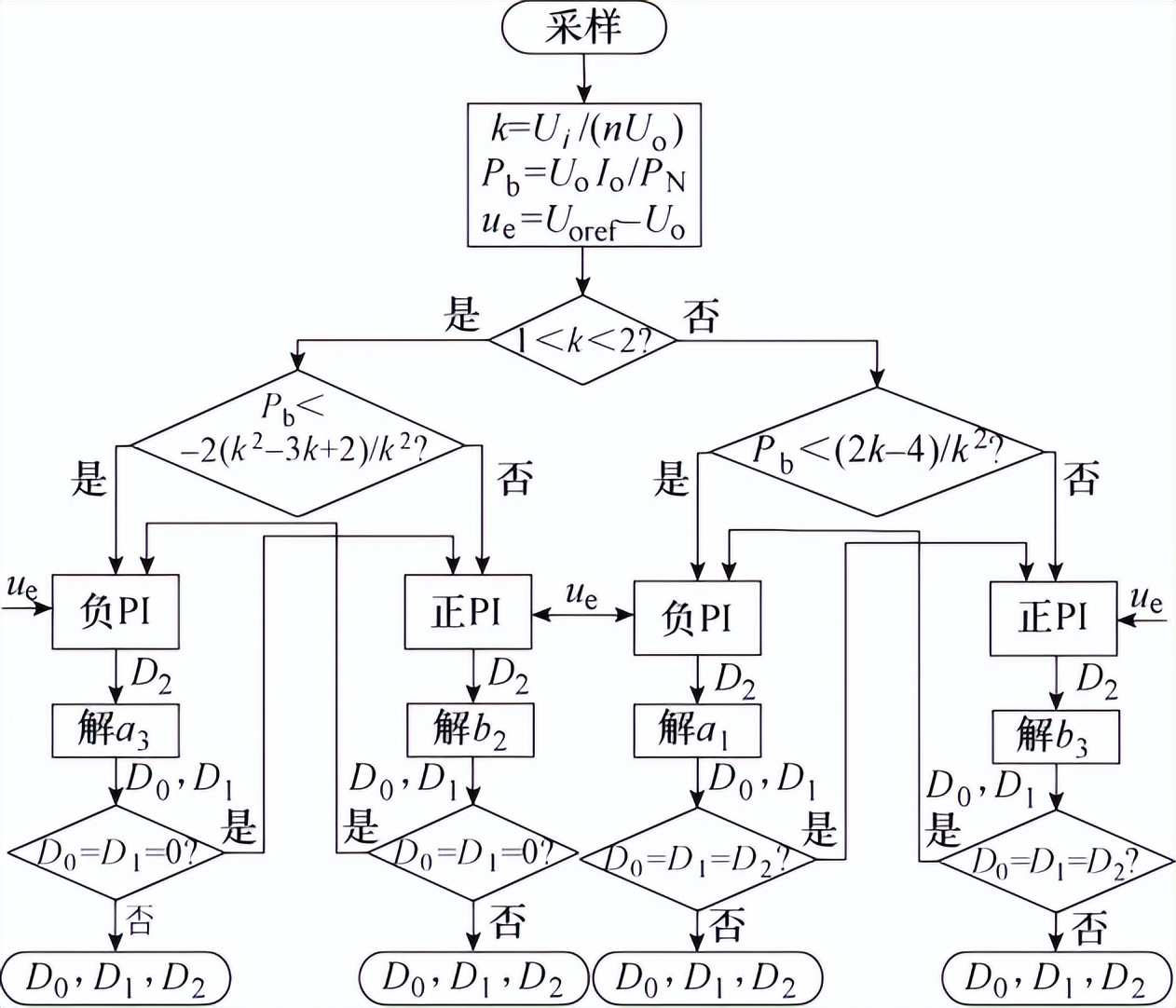
图3 全局最优工作点跟踪控制框图
结论
最后,研究人员通过设计一台实验样机来验证理论可行性。他们通过综合实验结果总结出所提出控制策略对比传统的优化策略,具备以下优势:
(1)三电平扩展移相控制在电压不匹配度较高的情况下能保持90%以上的传输效率,特别当Pb=0.5,电压转换比1<k<2时,传输效率可以始终保持在95%以上。
(2)在k =1.6、k =2.6,Pb改变时,电感电流有效值最小跟踪控制策略的传输效率始终高于电感电流峰值最小优化控制。


